Previous page     Contents     Next page

(Mg,Fe)O is the second most abundant mineral in the Earth's lower mantle, coexisting with (Mg,Fe)SiO₃ perovskite. Knowledge of the elastic properties in this solid solution is crucial for interpreting lower mantle seismic data in terms of bulk mineralogy.

Fe-bearing periclase is opaque, so optical measurements of the acoustic velocity such as Brillouin scattering are difficult to perform. Therefore, we performed a series of bench-top ultrasonic experiments on six synthetic single crystals of (Mg,Fe)O with Fe contents ranging from Fe/(Fe+Mg) = 0 to Fe/(Fe+Mg) = 0.75 and on Fe_1-xO end member (x=0.062). The (Mg,Fe)O samples were synthesised at 1450°C and 10^-7 atm oxygen fugacity. The Fe-content in each sample was determined by electron microprobe analysis at several points to ensure chemical homogeneity. The crystal thicknesses - determined visually with a high power microscope - range from 250 to 700 µm parallel to [100], and their orientation was verified by X-ray diffraction to be within 0.5° of the measured direction. Travel time data were collected in the 300-500 MHz frequency range. The velocity v is calculated by v = 2•l/t, with l sample thickness and t travel time. Sound wave velocity is related to the elastic modulus through the equation 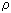• v²=c₁₁, with 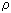density, v sound wave velocity and c₁₁ elastic modulus. The density 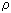of the different samples is inferred from lattice parameters measured by single crystal X-ray diffraction utilising the 8-reflection centering routine.

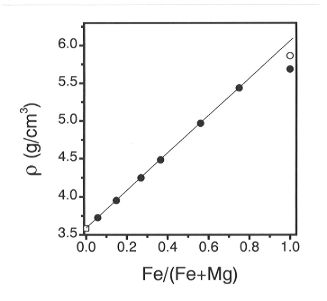
Figure 3.1-3 depicts the X-ray density as a function of Fe-content. The error bars in 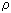and Fe/(Fe+Mg) are smaller than the symbols. All the data except non-stoichiometric Fe_0.938O give a linear trend of density versus Fe-content. The lower density for Fe_0.938 O presumably reflects the presence of about 6.2 atom% cation vacancies. If we recalculate this density by adjusting the mass so that all Fe-sites are occupied and correct the volume using extrapolation of the lattice constant data as a function of non-stoichiometry, we obtain a 'stoichiometric' density for FeO of 5.863 g/cm³. This value is shown as the open circle in Fig. 3.1-3. This 'stoichiometric' density is in reasonable agreement with the extrapolated trend on densities for samples with lower Fe-content.

Fig. 3.1-3: Density of (Mg, Fe)O as a function of Fe-content. The open circle represents the corrected stoichiometric' density of FeO. Error bars are within the symbols.

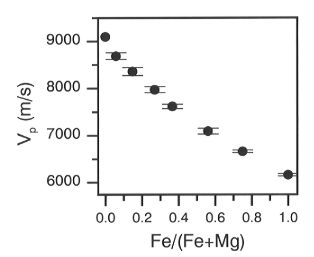
Figure 3.1-4a depicts the sound wave velocity v_p as a function of Fe-content. While the error bars in v_p include the uncertainties in both thickness and travel time measurements, they are dominated by the accuracy in thickness determination. The MgO end member value was taken from Jackson and Niesler .

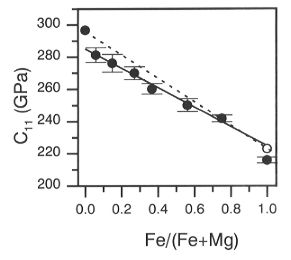
Figure 3.1-4b shows the elastic modulus c₁₁= • v². The error bars in c₁₁ include uncertainties in both the velocity and the density determination. The hollow circle represents the 'stoichiometric' FeO using the recalculated density. It is possible to fit a linear curve to the data points (solid line) except for the periclase value, which varies significantly from this trend. It can be seen that a simple linear interpolation of the data between the end-members periclase and wüstite, shown by the dotted line in Fig. 3.1-4b, deviates from our data.

We are currently performing experiments on (Mg,Fe)O of various compositions at higher pressures to determine the variation of the elastic properties with depth in the Earth.
 

Fig. 3.1-4a: Longitudinal sound wave velocity of (Mg,Fe) O as a function of Fe-content.	Fig. 3.1-4b: The elastic modulus c11 of (Mg,Fe)O as a function of Fe-content. The open circle represents the elastic modulus for the corrected 'stoichiometric' wüstite, the solid line is a linear fit through the (Mg,Fe)O data points, the dotted line is a linear interpolation between the two end-members.