

Considerable progress has been made in the theoretical understanding of the vibrational properties of silicate glasses. Most of the work done so far, however, is on the vibrational density of states (VDOS) of amorphous SiO2 (a-SiO2). Despite the fact that Raman and infra-red (IR) spectra are very sensitive probes of the local structure of amorphous materials, there have been only a few calculations of the Raman and IR spectra of a-SiO2. This is mainly due to the fact that the coupling coefficients linking these optical spectra with the VDOS are strong functions of the vibrational frequency.
Raman and IR spectra of binary and multi-component silicate glasses are considerably less well understood theoretically even with the enormous amount of experimental vibrational spectra published and the importance of these glasses to the material and earth sciences. Various empirical rules, established mainly by comparing Raman spectra of alkali silicate glasses and crystals, are currently used to relate, for example, the position and the intensity of the high-frequency bands in the range from 800 to 1200 cm-1 to the distribution of non-bridging oxygens (NBO). So far, there are only a few calculations on normal modes and the vibrational spectra of small isolated silicate units typical for depolymerized silicate glasses.
We have made the first realistic VDOS and Raman intensity calculations of Na2Si4O9 glass (denoted hereafter NS4) using a Kirkwood-type potential allowing us to compare the character of the vibrational modes in depolymerized alkali silicate glasses with amorphous SiO2. We have chosen the NS4 composition because it can serve as a simple model for more complicated multi-component high-silica glasses and its structure as well as vibrational spectra have been intensively studied by neutron diffraction, reverse Monte Carlo simulations, Raman and nuclear magnetic resonance (NMR) spectroscopy.
Computer models with periodic boundary conditions were first generated
by molecular dynamics (model NS4_I) and reverse Monte Carlo simulations
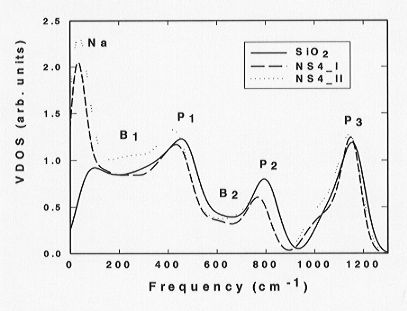
(model NS4_II). Division of the VDOS of a-SiO2 and NS4 glasses
into bands with different stretching character, participation ratio, bridging-oxygen
motion as well as phase quotient is illustrated in Fig. 3.6-1. The band
edges are shown to correspond to strongly localized modes. With increasing
degree of depolymerization the general character of the vibrational modes
qualitatively remains the same, which implies that the vibrational properties
of silicate glasses are a completely local phenomena reflecting the rigidity
of the SiO4 tetrahedra.
 |
|
|
The calculated Raman spectra for the NS4 glass are, generally, in good agreement with experiment (Fig. 3.6-2). The VV polarized Raman spectra arise mainly from bond-stretching scattering mechanisms that depend on the derivative of the parallel bond polarizability. On the contrary, the depolarized VH spectra arise from mixed bond-stretching and bond-bending scattering mechanisms. The calculations show that the perpendicular polarizability of the silicon - bridging oxygen bonds is an order of magnitude smaller than the derivative of the parallel bond polarizability and that their ratio is not affected by the presence of short-range disorder or depolymerization.
Partial Raman spectra of short-range units composed of different numbers
of non-bridging oxygens (Q-species) in the Na2Si4O9
glass were calculated and compared with empirically established rules for
determination of Q-speciation from polarized Raman measurements. We do
observe that the Q3 species give rise to a strong polarized
band with a maximum at about 1095 cm-1 and a shoulder at about
1010-1050 cm-1 as commonly interpreted. Similarly, the Q2
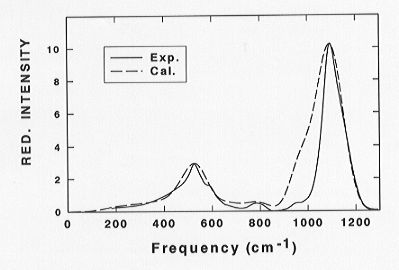 |
|
|
species exhibit a well resolved peak at about 950 cm-1. However, the shapes of the Q3 and Q2 peaks are in fact rather complex and conventional decomposition into symmetric Gaussian contributions seems to be an oversimplification. A detailed discussion of the implications of the present simulations for the interpretation of the Raman spectra of alkali silicate glasses and melts requires additional calculations of VDOS and the Raman spectra on glass models with a larger range of compositions. Such calculations are in progress.

Tel: +49-(0) 921 55 3700 / 3766, Fax: +49-(0) 921 55 3769, E-mail: bayerisches.geoinstitut(at)uni-bayreuth.de
 Previous page
Previous page